Iškilioji daugiakampiai. Apibrėžimas išgaubto daugiakampio. Iškilioji daugiakampio įstrižainė

Šie geometriniai skaičiai mus supa visur. Iškilioji daugiakampiai yra natūralūs, pavyzdžiui, bičių sultiniai arba dirbtiniai (sukurti žmonėmis). Šie skaičiai naudojami įvairių tipų dangų gamybai, tapybai, architektūrai, dekoracijoms ir kt. Iškilioji daugiakampiai turi savybę, kad visi jų taškai yra vienoje linijos pusėje, einančios per porą gretimų šios geometrinės figūros viršūnių. Yra ir kitų apibrėžimų. Išgaubtas yra tas daugiakampis, kuris yra vienoje puslankioje bet kurioje eilutėje, kurioje yra viena iš jo pusių.

Iškilioji daugiakampiai

Pradinės geometrijos metu visadames laikome tik paprastus daugiakampius. Norėdami suprasti visas geometrinių figūrų savybes, būtina suprasti jų prigimtį. Pirmiausia reikia suprasti, kad bet kuri linija, kurios galai sutampa, yra vadinamos uždarytos. Ir jo sukurta figūra gali turėti įvairių konfigūracijų. Daugiakampis yra paprasta uždara daugiakampė linija, kurios gretimos nuorodos neatitinka tos pačios linijos. Jo nuorodos ir smailės yra atitinkamai šios geometrinės figūros pusės ir viršūnės. Paprastoji polilinija neturi turėti savitakių sankirtų.

Daugiakampio viršūnės yra vadinamos gretimomisjei jie reiškia vienos iš jo pusių galus. Geometrinis skaitmuo, turintis n-ąjį viršūnių skaičių, taigi ir n-tas skaičius pusių, vadinamas n-gonu. Pati skaldyta linija vadinama šios geometrinės figūros riba ar kontūra. Daugiakampio plokštuma ar plokštumos daugiakampis vadinamas galutine bet kurios jam ribotos plokštumos dalimi. Šios geometrinės figūros kaimyninės pusės yra sujungtos linijos segmentai, prasidedantys nuo vienos viršūnės. Jie nebus kaimyniški, jei jie ateis iš skirtingų daugiakampio viršūnių.

Kiti konvejų daugiakampių apibrėžimai

Elementarioje geometrijoje yra keletas kitųekvivalentas apibrėžimų prasme, nurodant, kuris daugiakampis vadinamas išgaubtas. Ir visos šios formuluotės yra vienodai teisingos. Išgaubtas daugiakampis laikomas:

• kiekvienas segmentas, kuris jungia bet kuriuos du taškus viduje, visiškai jame;

• joje yra visos jos įstrižainės;

• bet koks vidinis kampas neviršija 180 °.

Daugiakampis visada padalija plokštumą 2dalys. Vienas iš jų yra ribotas (jis gali būti įtrauktas į ratą), o kitas - neribotas. Pirmasis vadinamas vidine sritimi, o antrasis vadinamas išoriniu šio geometrinio figūros regionu. Šis daugiakampis yra kelių puslankių sankirta (kitaip tariant - bendra sudedamoji dalis). Tokiu atveju kiekvienas segmentas, kurio pabaigoje yra taškai, priklausantys daugiakampiui, priklauso jam.

Išgaubtų daugiakampių veislės

Iškilioji daugiakampio apibrėžtis nenurodoį tai, kad yra daugybė rūšių. Ir kiekvienas iš jų turi tam tikrus kriterijus. Taigi, išgaubti daugiakampiai, kurių vidinis 180 ° kampas yra vadinamas silpnai išgaubtas. Išgaubtas geometrinė figūra, kad turi tris pikus, yra vadinamas trikampis, keturi - ketursieniu, penkių - poentagon ir tt Kiekvienas iš išgaubto n-gons atitinka šiuos svarbius reikalavimus: .. N turi būti lygi arba didesnė negu 3. Kiekvienas iš trikampių yra išgaubtas. Tokio tipo geometrinis figūras, kuriose visi viršūniai yra viename apskritime, vadinamas užrašu apskritime. Apibūdinamas vadinamas išgaubtas daugiakampis, jei jo kraštai šalia apskritimo liečia jį. Dvi daugiakampiai vadinami vienodais, jei juos galima sujungti su perdangos pagalba. Daugiakampio plokštuma vadinama plokščiu daugiakampiu (plokštumos dalimi), kurią riboja šis geometrinis skaičius.

Reguliarus išgaubtas daugiakampis

Pateikiami teisingi daugiakampiaigeometriniai skaičiai su vienodais kampais ir šonais. Jame yra 0 taškas, kuris yra to paties atstumo nuo kiekvieno jo viršūnių. Tai vadinama šios geometrinės figūros centru. Linijų, jungiančių centrą su geometrinio figūra viršūnių vadinamas apothem, ir tie, kurie prijungti 0 taškas su šalimis - spindulys.

Teisingas keturkampis yra kvadratas. Dešinysis trikampis vadinamas pusiausvyra. Tokiems skaičiams taikoma ši taisyklė: kiekvienas išgaubto daugiakampio kampas yra 180 ° * (n-2) / n,

kur n yra šio išgaubaus geometrinio skaičiaus viršūnių skaičius.

Bet kurio paprasto daugiakampio plotas apibrėžiamas pagal formulę:

S = p * h

kur p yra lygus pusei visos tam tikro daugiakampio pusių sumos, o h yra lygus apophema ilgiui.

Iškilioji daugiakampiai ypatybės

Iškilioji daugiakampiai turi tam tikrų savybių. Taigi, segmentas, kuris jungia bet kuriuos du tokio geometrinio taško taškus, būtinai yra jame. Įrodymas:

Tarkime, kad P yra išgaubtasdaugiakampis Paimkite du savavališkai taškų, pavyzdžiui, A ir B, kurie priklauso p dabartinės apibrėžimą cilindro formą, šie taškai yra vienoje pusėje tiesės, kurioje yra bet kuria kryptimi R. Todėl AB "taip pat turi šį objektą ir esančius R. cilindro formą visada Galima suskaidyti į keletą trikampių absoliučiai visomis įstrižomis, kurios yra ištrauktos iš vieno iš jo viršūnių.

Išgaubtų geometrinių figūrų kampai

Išgaubto daugiakampio kampai yra kampaisusiformuoja jos partijos. Vidiniai kampai yra šios geometrinės figūros vidinėje srityje. Kampas, kurį sudaro jos pusės, suvienodinamos vienoje viršūnėje, vadinamas išgaubto daugiakampio kampu. Kampai greta tam tikros geometrinės figūros vidinių kampų vadinami išoriniais. Kiekvienas jo viduje esančio išgaubto poligono kampas lygus:

180 ° - x,

kur x yra išorinio kampo vertė. Ši paprasta formulė taikoma bet kokiems tokio tipo geometriniams skaičiams.

Bendrais atvejais egzistuoja išoriniai kampaiši taisyklė: kiekvienas išgaubto daugiakampio kampas lygus 180 ° ir vidinio kampo vertės skirtumui. Jis gali turėti vertes nuo -180 ° iki 180 °. Todėl, kai vidinis kampas yra 120 °, išorinis kampas bus 60 °.

Išgaubtų daugiakampių kampų suma

Išgaubto daugiakampio vidinių kampų suma nustatoma pagal formulę:

180 ° * (n-2),

kur n yra n-gono viršūnių skaičius.

Apskaičiuojamas išgaubto daugiakampio kampų sumagana paprasta. Apsvarstykite bet kokį tokį geometrinį figūrą. Norėdami nustatyti kampų sumą viduje išgaubto daugiakampio, viena iš jos viršūnių turi būti prijungta prie kitų viršūnių. Dėl šio veiksmo gauname (n-2) trikampius. Žinoma, kad bet kurio trikampio kampų suma visuomet yra 180 °. Kadangi jų skaičius bet kuriame daugiakampyje yra lygus (n-2), tokio skaičiaus vidinių kampų suma yra 180 ° x (n-2).

Išgaubto daugiakampio kampų, t. Y.visi du vidiniai ir gretimi išoriniai kampai, šis išgaubtas geometrinis skaičius visada bus 180 °. Atsižvelgiant į tai, galima nustatyti visų jo kampų sumą:

180 x n.

Vidinių kampų suma yra 180 ° * (n-2). Atsižvelgiant į tai, visų nurodytų skaičių išorinių kampų suma nustatoma pagal formulę:

180 ° * n-180 ° - (n-2) = 360 °.

Bet kurio išgaubto daugiakampio išorinių kampų suma visada bus 360 ° (nepriklausomai nuo jo šonų skaičiaus).

Išgaubto daugiakampio išorinis kampas paprastai yra 180 ° ir vidinio kampo vertės skirtumas.

Kitos išgaubto daugiakampio savybės

Be pagrindinių geometrinių savybiųskaičiai, jie turi kitus, kurie atsiranda manipuliuoti su jais. Taigi, bet kurį iš daugiakampių galima suskirstyti į keletą išgaubtų n-gonų. Tam reikia tęsti kiekvieną savo pusę ir supjaustyti šį geometrinį figūrą išilgai šių tiesių linijų. Supjaustykite bet kurį daugiakampį į kelias išgaubtas dalis ir tokiu būdu, kad kiekvieno gabalo viršūnės sutampa su visais jo viršūnėmis. Iš šio geometrinio skaičiaus labai paprasta padaryti trikampius, laikydami visas įstrižas iš vienos viršūnės. Taigi, bet koks daugiakampis, galutinis rezultatas, gali būti suskirstytas į tam tikrą skaičių trikampių, o tai yra labai naudinga sprendžiant įvairias problemas, susijusias su tokiais geometriniais skaičiais.

Išgaubto daugiakampio perimetro

Polilinijos gabalai, vadinami šonaisdaugiakampis, dažniausiai žymimas šiais raidėmis: ab, bc, cd, de, ea. Tai geometrinio figūros pusės su viršūnėmis a, b, c, d, e. Viso šio išgaubto daugiakampio pusių ilgių suma yra vadinama jo perimetru.

Daugiakampio ratas

Iškilioji daugiakampiai gali būti įrašyti iraprašyta. Į jį įtraukiamas apskritimas, liečiantis visas geometrinio figūros puses. Toks daugiakampis vadinamas aprašytu. Daugiakampyje užrašytas apskritimo centras yra visų kampų susikirtimo taškas per tam tikrą geometrinę figūrą. Tokio daugiakampio plotas lygus:

S = p * r,

kur r - įterpto apskritimo spindulys, o p - tai pusrutulys iš nurodyto daugiakampio.

Ratas, kuriame yra daugiakampio viršūnės,vadinamas apibūdintas šalia jo. Šiuo atveju šis išgaubtas geometrinis skaičius yra vadinamas užrašu. Apskritimo centras, apibūdintas netoli tokio daugiakampio, yra taškas, vadinamasis visų pusių vadinamųjų vidurinių statmenų sankirta.

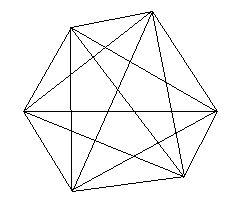
Iškilioji geometrinių figūrų įstriža

Iškilioji daugiakampio įstrižainė yra segmentai,kuris jungia ne gretimus viršūnius. Kiekvienas iš jų yra šios geometrinės figūros viduje. Tokio n-gono įstrižainių skaičius nustatomas pagal formulę:

N = n (n-3) / 2.

Žaidžia išgaubto daugiakampio įstrižainių skaičiussvarbų vaidmenį elementarioje geometrijoje. Trikampių skaičius (K), į kurį galima išdalyti kiekvieną išgaubtą daugiakampį, apskaičiuojamas pagal šią formulę:

K = n - 2.

Išgaubto daugiakampio įstrižainių skaičius visada priklauso nuo jo viršūnių skaičiaus.

Iškilioji daugiakampio suskaidymas

Kai kuriais atvejais išspręsti geometrinįreikia išgaubtą daugiakampį padalinti į keletą trikampių su nesiskiriančiomis įstrižomis. Šią problemą galima išspręsti nustatant tam tikrą formulę.

Problemos apibrėžimas: mes vadiname tam tikrą išgaubto n-gono padalijimą į keletą trikampių, įstrižainių, kurie susikerta tik šios geometrinės figūros viršūniams.

Sprendimas: Tarkime, kad P1, P2, P3 ..., Pn yra šio n-gono viršūnės. Numeris Xn yra jo pertvarų skaičius. Mes atidžiai išnagrinėsime gaunamos įstrižainės geometrinį figūrą Pi Pn. Bet kuriame iš reguliarių pertvarų P1 Pn priklauso tam tikram trikampiui P1 Pi Pn, kurio 1 <i <n. Tuo remdamasis ir darant prielaidą, kad i = 2,3,4 ..., n-1, mes gauname (n-2) šių pertvarų grupes, į kurias įtraukiami visi galimi specialūs atvejai.

Tegul i = 2 yra viena reguliarios grupėskuris visada turi įstrižainę P2 Pn. Į ją įeinančių pertvarų skaičius sutampa su (n-1) -gon P2 P3 P4 ... Pn skirtumų skaičiumi. Kitaip tariant, jis lygus Xn-1.

Jei i = 3, tada ši kita grupių pertvarų busvisada yra įstrižainių P3 P1 ir P3 Pn. Be to, reguliarių pertvarų, esančių šioje grupėje, skaičius sutampa su pertvaros (n-2) -gon P3 P4 ... Pn skaičiumi. Kitaip tariant, jis bus lygus Xn-2.

Leiskite i = 4, tada tarp trimatės reguliariaipertvarų, be abejo, yra trikampis P4 P1 PN, kuri bus Ribojasi keturkampį P1 P2 P3 P4, (N-3) -Gon P5 P4 ... PN. Teisingų pertvaros skaičius toks, keturkampis lygus X4, ir pertvarų skaičius (n-3) -Gon lygus Xn-3. Remiantis tuo, kas išdėstyta, galima sakyti, kad iš viso reguliariai pertvaros, kurios yra pateiktos šioje grupėje lygus Xn-3 X4. Kitos grupės, kurioje i = 4, 5, 6, 7 ... bus pateikta 4 Xn-X5, Xn-5 "X6, Xn-6 ... X7 reguliariai pertvaros.

Tegul i = n-2, tada reguliuojamų pertvarų skaičius tam tikroje grupėje sutampa su pertvarų skaičiumi grupėje, kurios i = 2 (kitaip tariant, ji lygi Xn-1).

Kadangi X1 = X2 = 0, X3 = 1, X4 = 2 ..., tada visų išgaubto daugiakampio skirtumų skaičius yra lygus:

Xn = Xn-1 + Xn-2 + Xn-3 X4 + Xn-4 X5 + ... + X 5 Xn-4 + X4 Xn-3 + Xn-2 + Xn-1.

Pavyzdys:

X5 = X4 + X3 + X4 = 5

X6 = X5 + X4 + X4 + X5 = 14

X7 = X6 + X5 + X4 * X4 + X5 + X6 = 42

X8 = X7 + X6 + X5 * X4 + X4 * X5 + X6 + X7 = 132

Reguliuojamų pertvarų skaičius susikerta viena įstriža

Konkrečių atvejų patikrinime galima daryti prielaidą, kad išgaubtų n-gonų įstrižainių skaičius yra lygus visų dalių (n-3) pertvaroms.

Įrodyti šią prielaidą: mes atstovaujame, kad P1n = Xn * (n-3), tada bet kuris n-gonas gali būti suskaidytas į (n-2) -triangles. Tuo pačiu metu vienas iš jų gali būti sujungtas (n-3) - keturkampis. Be to, kiekvienas keturkampis turi įstrižainę. Kadangi šiame išgaubtame geometriškame paveiksle gali būti įterptos dvi įstrižainės, tai reiškia, kad bet kurią (n-3) dvigubą apskritimą galima įterpti papildomas įstrižas (n-3). Remiantis tuo galima daryti išvadą, kad bet kokioje reguliaraus pertvaroje galima atlikti (n-3) -diagononus, atitinkančius šios problemos sąlygas.

Iškilioji daugiakampiai plotai

Dažnai sprendžiant įvairias problemas, pagrindinisgeometrija, tampa būtina nustatyti išgaubto daugiakampio plotą. Tarkime, kad (Xi. Yi), i = 1,2,3 ... n yra koordinatės seka visų gretimų viršūnių daugiakampis, kuris neturi savikriukimo. Šiuo atveju jo plotas apskaičiuojamas pagal šią formulę:

S = 1 (Σ (X_i + X_{i + 1}) (Y_i + Y_{i + 1})),

kur (X₁, Y.₁) = (X_{n +1}, Y._{n + 1})

</ p>