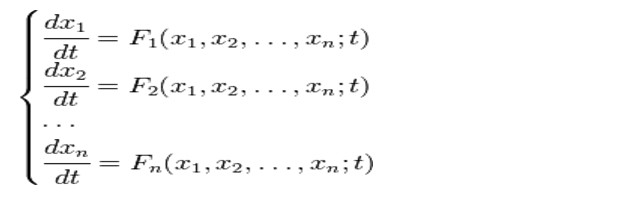Šiuolaikiniame moksle yra daugybė požiūriųsukurti kiekybinį bet kurios sistemos matematinį modelį. Ir vienas iš jų laikomas baigtinių elementų metodu, kuris grindžiamas diferencinės (begalybės mažo) elemento elgesio nustatymu, paremtu tariamu pagrindinių elementų, galinčių visiškai apibūdinti šią sistemą, ryšį. Taigi, ši technika naudoja diferencialines lygtis sistemos aprašyme.
Teoriniai aspektai

Teorinius metodus lemia finišo metodasSkirtumai, kurie yra šios skaičiavimo įrankių serijos protėvis ir yra plačiai naudojamos. Galutinio skirtumo metoduose jų taikymas bet kurioms diferencialinėms lygtoms yra ypač patrauklus. Tačiau dėl sudėtingos ir sudėtingos problemos ribinių sąlygų apskaitos programuojamumo yra tam tikrų apribojimų taikant šiuos metodus. Sprendimo tikslumas priklauso nuo tinklelio lygio, kuris apibrėžia mazgų taškus. Todėl, sprendžiant tokio pobūdžio problemas, dažnai reikia apsvarstyti sistemas aukštesniųjų алгебраических lygtis.

Galutinių elementų metodas yra pasiektas metodaslabai aukštas tikslumo lygis. Ir šiandien daugelis mokslininkų pažymi, kad dabartiniame etape nėra analogiško metodo, galinčio pasiekti tų pačių rezultatų. Galutinių elementų metodas turi platų taikomumą, efektyvumą ir paprastumą, su kuriuo atsižvelgiama į konkrečias ribines sąlygas, todėl galima tapti rimtu konkurentu bet kokiam kitam metodui. Tačiau, be šių privalumų, jam būdingi trūkumai. Pavyzdžiui, tai yra pavyzdžių atrankos schema, dėl kurios neišvengiamai naudojamas daugybė elementų. Ypač, jei kalbame apie trimatis problemas, turinčias nuotolines ribas, ir kiekvienoje iš jų atsiranda tęstinumas visiems nežinomiems kintamiesiems.
Alternatyvus požiūris
Kaip alternatyva kai kuriems mokslininkamsSiūloma kitokiu būdu naudoti analitinę diferencialinių lygčių sistemos integraciją arba įvesti tam tikrą aproksimaciją. Bet kokiu atveju, koks metodas yra naudojamas, pirmiausia reikia integruoti diferencialinę lygtį. Pirmuoju problemos sprendimo etapu būtina transformuoti diferencialines lygtis į integralių analogų sistemą. Ši operacija leidžia mums gauti lygčių sistemą, turinčią tam tikro regiono vertes.

Kitas alternatyvus metodas yra metodasribiniai elementai, kurių plėtojimas grindžiamas integralių lygčių idėja. Šis metodas yra plačiai naudojamas be kiekvieno atskiro sprendimo unikalumo įrodymų, dėl kurio jis tampa labai populiarus ir realizuojamas naudojant kompiuterines technologijas.
Taikymo sritis
Galutinių elementų metodas yra gana sėkmingai naudojamas kartu su kitais skaitiniais metodais mišrioje formuluotėje. Šis derinys leidžia išplėsti jo taikymo sritį.
</ p>