Kaip išspręsti tiesios linijos lygtį per du taškus?

Matematika nėra nuobodus mokslas, kaip kartais atrodo. Yra daug įdomių, nors kartais nesuprantamų tiems, kurie nenori to suprasti. Šiandien aptarsime vieną iš labiausiai paplitusių ir paprastas faktas, matematikos, bet, kad jos lauke, kad nuo algebros ir geometrijos slenksčio. Pakalbėkime apie tiesiogines ir jų lygtis. Atrodytų, kad tai yra nuobodus mokyklos dalykas, kuris nieko neįstengia įdomiai ir naujo. Tačiau tai nėra taip, ir šiame straipsnyje mes stengsimės įrodyti jums savo požiūrį. Prieš išvykdami į įdomiausias ir apibūdinti linija lygtį per dviejų taškų, mes pažvelgti į visų šių matavimų istoriją, ir tada išsiaiškinti, kodėl visa tai buvo būtina, ir kodėl dabar negadina žinant šias formules.

Istorija

Net senais laikais matematikai buvo malonugeometrines konstrukcijas ir visus grafikų tipus. Šiandien sunku pasakyti, kas pirmą kartą sugalvojo tiesią liniją per du taškus. Bet galime manyti, kad šis žmogus buvo Euklidas - senovės graikų mokslininkas ir filosofas. Tai buvo tas, kuris savo traktate "Pradžioje" atsirado būsimos Euklido geometrijos pagrindą. Dabar šis matematikos skyrius yra laikomas pasaulio geometrinio reprezentavimo pagrindu ir mokomas mokykloje. Tačiau reikia pasakyti, kad Euklido geometrija trimačiame matavime veikia tik makro lygiu. Jei mes vertiname kosmosą, ne visada įmanoma reprezentuoti visus reiškinius, kurie ten atsiranda.

Po Euklido buvo ir kiti mokslininkai. Ir jie tobulino ir suprato tai, ką atrado ir parašė. Galų gale pasirodė stabili geometrijos sritis, kurioje viskas vis dar nesugebama. Ir tūkstantmečiams buvo įrodyta, kad lygiagreta linija per du taškus yra labai lengva surinkti. Bet prieš pradėdami paaiškinti, kaip tai padaryti, aptarsime šiek tiek teorijos.

Teorija

Ši linija yra begalinė abiem kryptimisSegmentas, kurį galima suskirstyti į begalinį skaičių bet kokio ilgio segmentų. Siekiant reprezentuoti tiesią liniją, dažniausiai naudojami grafikai. Ir grafikai gali būti ir dvimačio, ir trimačio koordinačių sistemoje. Jie pastatyti pagal jiems priklausančių taškų koordinates. Galų gale, jei pažvelgsite į tiesią liniją, pamatysite, kad ji susideda iš begalybės taškų.

Tačiau yra kažkas, kad linija yra labai stipriskiriasi nuo kitų tipų linijų. Tai jos lygtis. Apskritai, tai yra labai paprasta, skirtingai tariant, apskritimo lygtis. Žinoma, kiekvienas iš mūsų išlaikė mokyklą. Bet vis tiek rašykite bendrą formą: y = kx + b. Kitame skyriuje mes išsamiai aptarsime, kas reiškia kiekvieną iš šių raidžių ir kaip išspręsti šią paprastą tiesią liniją, einančią per du taškus.

Linijos lygtis

Lygybė, kuri buvo pateikta aukščiau, iryra reikalinga linijos lygtis. Verta paaiškinti, ką čia reiškia. Kaip jūs galite atspėti, y ir x yra kiekvieno taško, kuris priklauso tiesiai, koordinatės. Apskritai, ši lygtis egzistuoja tik todėl, kad kiekvienam bet kurios eilutės taškui yra savotiška susieti su kitais taškais, taigi yra ir teisė, jungianti vieną koordinatę su kita. Šis įstatymas nustato, kaip tiesios linijos lygtis atrodo per du taškus.

Kodėl du taškai? Visa tai yra todėl, kad minimalus taškų skaičius, reikalingas tiesios linijos statybai dvimačioje erdvėje, yra du. Jei mes priimsime erdvę erdvėje, tada vienos tiesiosios linijos statybai reikalingų taškų skaičius taip pat bus lygus dviems, nes trys taškai jau yra plokštuma.

Taip pat yra teorema, įrodanti, kad galima išgauti vieną tiesią liniją per du savavališkai taškus. Šis faktas gali būti patikrintas praktiškai, derinant du atsitiktinius taškus grafike su valdikliu.

Dabar apsvarstykite konkretų pavyzdį ir parodykite, kaip išspręsti šią baisią lygtį tiesios linijos, einančios per du taškus.

Pavyzdys:

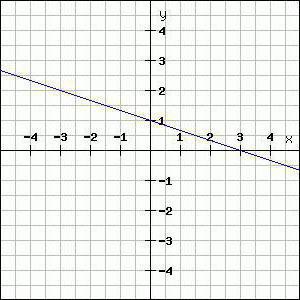
Apsvarstykite du taškus, per kuriuos norite statyti tiesią liniją. Mes suteikiame jiems koordinates, pvz., M₁(2; 1) ir M₂(3; 2). Kaip mes žinome iš mokyklos kurso, pirmoji koordinatė yra vertė išilgai OX ašies, o antrasis yra palei OY ašį. Pirmiau pateikta lygiagreti tiesioji linija per du taškus, ir norint sužinoti trūkstamus parametrus k ir b, turime surinkti dviejų lygčių sistemą. Tiesą sakant, ji bus sudaryta iš dviejų lygčių, kiekviena iš jų turės dvi iš mūsų nežinomų konstantų:

1 = 2k + b

2 = 3k + b

Dabar pats svarbiausias dalykas - išspręsti šią sistemą. Tai daroma gana paprasta. Pirma, mes išreikšti iš pirmosios lygties b: b = 1-2k. Dabar mes turime pakeisti gautą lygtį į antrąją lygtį. Tai daroma pakeičiant b lygybe, kurią gavo mes:

2 = 3k + 1-2k

1 = k;

Dabar mes žinome, kokia vertėkoeficientas k, atėjo laikas sužinoti kitos konstanta - b vertę. Tai dar lengviau. Kadangi mes žinome b priklausomybę k, mes galime pakeisti pastarosios vertę į pirmąją lygtį ir sužinoti nežinomą vertę:

b = 1-2 * 1 = -1.

Žinodami abu koeficientus, dabar galime jas pakeistiį pradinę bendrą lygtį tiesios linijos per du taškus. Taigi, mūsų pavyzdyje gauname tokią lygtį: y = x-1. Tai yra norima lygybė, kurią turėtume įgyti.

Prieš pradėdami daryti išvadą, aptarkime šio matematikos skyriaus taikymą kasdieniame gyvenime.

Paraiška

Kaip tokia, tiesiosios linijos per lygtįdu taškai nerandate. Bet tai nereiškia, kad mums to nereikia. Fizikos ir matematikos požiūriu labai aktyviai naudojamos iš jų esančių linijų ir savybių lygtys. Jūs netgi negalite to pastebėti, bet mus supa matematika. Netgi tokios akivaizdžiai nematomos temos, kaip tiesios linijos lygtis per du taškus, yra labai naudingos ir labai dažnai taikomos esminiu lygmeniu. Jei iš pirmo žvilgsnio atrodo, kad tai niekur negali išeiti, tu esi klaidinga. Matematika ugdo loginį mąstymą, kuris niekada nebus nereikalingas.

Išvada

Dabar, kai mes supratome, kaip kurti linijas du kartus, mums nereikia atsakyti į visus su tuo susijusius klausimus. Pavyzdžiui, jei mokytojas jums sako: "Parašykite lygiagrečią tiesią liniją, einančią per du taškus ", tada jūs negalėsite tai padaryti, tikimės, kad šis straipsnis jums buvo naudingas.